В чем суть — два товарища из Сан-Франциского ФЕДа (Zheng Liu — a research advisor in the Economic Research Department of the Federal Reserve Bank of San Francisco и Mark M. Spiegel — a vice president in the Economic Research Department of the Federal Reserve Bank of San Francisco), решили провести исследование на тему того, как влияет отношение стареющего населения на P/E. Конкретно в качестве коэффициента старения они взяли логарифм отношения группы 40–49 лет к 60–69 далее M/O.
Оригинальная статья авторов Zheng Liu и Mark M. Spiegel размещена
здесь.
Перевод статьи от
slon.ru размещен здесь.
Ниже представлена оригинальная картинка из их расчета. Красным — PE, синим — этот коэффициент; слева — исторические данные, справа — предсказание модели.
Теперь они нам утверждают:
Quote:«Statistical analysis confirms this correlation. In our model, we obtain a statistically and economically significant estimate of the relationship between the P/E and M/O ratios. We estimate that the M/O ratio explains about 61% of the movements in the P/E ratio during the sample period. In other words, the M/O ratio predicts long-run trends in the P/E ratio well. »
«Статистический анализ подтвердил эти корреляции. В нашей модели мы получили статистические и экономически значимые оценки взаимосвязи между P/E и M/O(коэффициент старения). Мы оценили, что M/O отношения ОБЪЯСНЯЕТ БОЛЕЕ 61% ДВИЖЕНИЯ В P/E за заданныq период. Другими словами, M/O соотношение предсказывает долгосрочные тренды в P/E.»
Собственно, первая мысль, которая возникла и в дальнейшем нашла подтверждение — они опять прогуляли в институте курсы по эконометрике и посчитали корреляцию двух процессов. Чтобы подтвердить гипотезу, пришлось скачать их данные и воспроизвести коэффициенты (та же самая картинка что у них, с кружочками — P/E, без M/O):
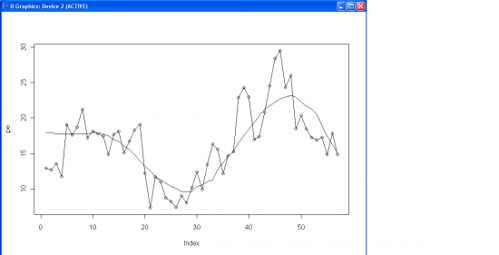
Теперь, добравшись до данных, считаем статистически корректно ранковую корреляцию приращений между двумя процессами. Получаем 0.15 (15%) при уровне статистической значимости 90% (то есть вероятность, что данная взаимосвязь получилась чисто случайно составляет ~10%, но это нормально, учитывая малый размер выборки). Прямой тест на коинтеграцию неприменим, так как процессы не unit root (то есть не интегралы белого шума), хотя и близки к нему. Но можно построить линейной регрессией спред, а дальше проверить, насколько статистически значима ECM (error-correction model) репрезентация. Результат получается схожий: значимость вклада спреда в приращения P/E выходит за границы статистической значимости (70%-ая вероятность того, что результат получен чисто случайно).
На рисунке ниже по горизонтали изображены приращения P/E, по вертикали — приращения M/O.
В общем, не верьте глазам своим. Несмотря на то, что кажется будто взаимосвязь между ними значительная, если посчитать ее статистически корректно она будет в районе 15% при не высоком уровне статистической значимости. А товарищам из FRBSF должно быть стыдно за то, что они внесли очередной вклад в поток псевдо-экономического шлака, от которого и так уже некуда деваться.
Данные и скрипты Вы можете
скачать здесь.